支持向量机（SVM）是90年代中期发展起来的基于统计学习理论的一种机器学习方法，通过寻求结构化风险最小来提高学习机泛化能力，实现经验风险和置信范围的最小化，从而达到在统计样本量较少的情况下，亦能获得良好统计规律的目的。

通俗来讲，它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，即支持向量机的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

由简至繁支持向量机(support vector machine,SVM)可分类为三类：

线性可分（linear SVM in linearly separable case）的线性SVM
线性不可分的线性SVM
非线性（nonlinear）SVM

也可以称为：

hard-margin SVM
soft-margin SVM
kernel SVM

什么是线性可分

给定一个数据集，如果存在某个超平面$w^T \cdot x + b = 0$能将测试机的正实例和负实例完全正确的划分到超平面两侧，即

$\left\{ \begin{array} { l l } { w^T \cdot x_i +b > 0 } & { y_i = +1 } \\ { w^T \cdot x_i +b < 0 } & { y_i = -1 } \end{array} \right.$

称数据集为线性可分数据集（linearly separable data set）否则，称为线性不可分数据集

如何找到这个超平面呢？

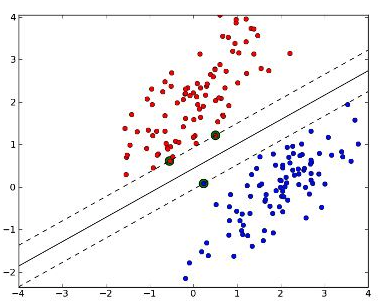
对于一个数据集，可能有很多的线来分割,直观来看，黄色这条线应该是适应性最好的，离直线两边的数据的间隔最大，对训练集的数据的局限性或噪声有最大的“容忍”能力。

为什么叫SVM

怎么找到这个平面呢？将距离分离超平面最近的两个不同类别的样本点称为支持向量（Support Vector）的，构成了两条平行于分离超平面的长带，二者之间的距离称之为Margin。显然，Margin更大，则分类正确的确信度更高（与超平面的距离表示分类的确信度，距离越远则分类正确的确信度越高）。

SVM就是求解支持向量的，所以叫支持向量机。

间隔

那么找到这个平面的问题就转换成了，怎么找到这个最大Margin。找到这个Margin就要知道间隔的定义了。
间隔分为函数间隔 (functional margin) 和几何间隔 (geometric margin)

函数间隔

函数间隔的定义为

$\hat { \gamma } = y \left( \boldsymbol { w } ^ { \mathrm { T } } \boldsymbol { x } + b \right) = y f ( \boldsymbol { x } )$

函数间隔其实就是类别标签乘上了f(x)的值，可以看到，该值永远是大于等于0的，正好符合了距离的概念，距离总不能是负的吧。

函数间隔越大, 代表我们对于分类的结果非常确定. 我们希望函数间隔越大越好. 看上去好像没什么毛病, 但这里的确有一个问题, 就是其实我们可以在不改变这个超平面的情况下可以让函数间隔任意大, 为什么?

由超平面的解析式：

$w^Tx+ b=0$

方程两边同时乘以常数 C，即

$C\ w^Tx+ C\ b=0$

显然以上两个方程的解是一致的，超平面没有发生变化。换句话说，参数 w 和 b 同比例缩放对超平面并没有影响。然而参数 w 和 b 放大或缩小 C 倍，函数间隔：

$\hat\gamma = y(Cw^Tx + Cb) = Cy(w^Tx + b)=C \hat\gamma$

这意味着函数间隔 $\hat \gamma$ 也会放大和缩小相同的倍数。

而几何间隔：

$\tilde \gamma = \frac{C\hat\gamma}{C||w||_2} = \tilde \gamma$

这意味着几何间隔不变。

为了解决这个问题, 我们就需要加上一些限制条件,所以，需要将$w$的大小固定，如$||w||=1$，使得函数间隔固定。这时的间隔也就是几何间隔 .(看完后面几何间隔的定义就明白了)

几何间隔

对二维空间来说,点$P(x_0,y_0)$到直线$ax+by+c=0$的公式是

$\mathrm { d } = \frac { \left| a x _ { 0 } + b y _ { 0 } + c \right| } { \sqrt { a ^ { 2 } + b ^ { 2 } } }$

高维空间呢？

$\gamma = \frac { y \left( w ^ { T } x + b \right) } { \| w \| _ { 2 } }$

这个式子是怎么推导出来的

对于超平面$w^Tx+b$，$x$在超平面上的投影是$x_0$,$w$是超平面的法向量，那么有

$x = x_0 + \gamma \frac {w}{||w||}$

那么

$f(x) = f(x_0 + \gamma \frac {w}{||w||}) \\ =w^Tx_0+w^T\gamma \frac {w}{||w||}+b \\ =f(x_0)+w^T\gamma \frac {w}{||w||} \\ =0 +\gamma \frac {w^Tw}{||w||} \\ =\gamma \frac {||w||^2}{||w||} \\ =\gamma||w|| \\ \Downarrow \\ \gamma=\frac{f(x)}{||w||}$

这里的$\gamma$其实是带符号的，我们需要的是绝对值，乘上对应的类别 y 即可，因此实际上我们定义几何间隔为：

$\tilde { \gamma } = y \gamma = \frac { \hat { \gamma } } { \| \boldsymbol { w } \| }$

也就是上面的

$\frac { y \left( w ^ { T } x + b \right) } { \| w \| _ { 2 } }$

函数间隔$y(w^Tx+b)=yf(x)$实际上就是 $|f(x)|$ ，只是人为定义的一个间隔度量；而几何间隔$\frac{|f(x)|}{||w||}$才是直观上的点到超平面距离。

间隔我们也知道了，所以我们可以求这个Margin了

上面说过，对于超平面来说函数间隔其实并不固定，所以我们不妨设$\hat y = 1$,那么几何间隔就是 $\frac {1}{||w||}$,最大化这个几何间隔就是最小化$||w||$即可.

另外一种推法：

设Margin为 $2\lambda$ 对于任意正样本 $x_+$ ，负样本$ x_- $来说

$\left\{ \begin{array} { l } { w^T \cdot x_+ +b \ge \lambda} \\ { w^T \cdot x_- +b \le -\lambda } \end{array} \right. \ \ \ \ \ \ y_i= \left\{ \begin{array} { l r } { +1 } & {x_+} \\ { -1 } & {x_-} \end{array} \right.$

结合一下

$y_i(w^Tx_i+b)-\lambda \ge 0$

距离其实就是 $x_+-x_-$ 在法向量 $w$ 上的投影

$\frac {(x_+-x_-)w^T}{|w|} \\ w \ \ w^T都是表示的法向量，一个是行表示一个是列表示$

把上面式子代进去

$\frac {(\lambda-b)+(\lambda+b)}{|w|} \\ \Downarrow \\ \frac {2\lambda}{||w||} \\ 注: |w| = ||w||_2 = \sqrt{w_1^2 + w_2^2 + \cdots}\\$

所以就是求这个最大的Margin了，也就是

$max(\frac{1}{||w||}) \\ \Downarrow \\ min(||w||) \\ \Downarrow \\ min (\frac{1}{2}||w||_2^2) \qquad s.t \;\; y_i(w^Tx_i + b) \geq 1 (i =1,2,...m) \\$

转化为拉格朗日函数

$\mathcal { L }(w,b,\alpha) = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1] \qquad s.t \ \alpha_i \geq 0 \\$

也就是求这个函数的极值

$L' = (\frac{\partial{L}}{\partial{w}},\frac{\partial{L}}{\partial{b}}) \\ \frac{\partial{L}}{\partial{w}}=0 \Rightarrow w^T-\sum_i\alpha_iy_ix_i=0 \\ \frac{\partial{L}}{\partial{b}}=0 \Rightarrow \sum_i\alpha_iy_i=0$

代回去

$\begin{align} \min _ { w , b } \max _ { \alpha _ { i } \geq 0 } \mathcal { L } ( w , b , \alpha ) & = \frac{1}{2}||w||_2^2 - \sum\limits_{i=1}^{m}\alpha_i[y_i(w^Tx_i + b) - 1] \\ & = \frac{1}{2}w^Tw-\sum\limits_{i=1}^{m}\alpha_iy_iw^Tx_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\ & = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i -\sum\limits_{i=1}^{m}\alpha_iy_iw^Tx_i - \sum\limits_{i=1}^{m}\alpha_iy_ib + \sum\limits_{i=1}^{m}\alpha_i \\ & = \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i - b\sum\limits_{i=1}^{m}\alpha_iy_i + \sum\limits_{i=1}^{m}\alpha_i \\ & = - \frac{1}{2}w^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i + \sum\limits_{i=1}^{m}\alpha_i \\ & = -\frac{1}{2}(\sum\limits_{i=1}^{m}\alpha_iy_ix_i)^T(\sum\limits_{i=1}^{m}\alpha_iy_ix_i) + \sum\limits_{i=1}^{m}\alpha_i \\ & = -\frac{1}{2}\sum\limits_{i=1}^{m}\alpha_iy_ix_i^T\sum\limits_{i=1}^{m}\alpha_iy_ix_i + \sum\limits_{i=1}^{m}\alpha_i \\ & = -\frac{1}{2}\sum\limits_{i=1,j=1}^{m}\alpha_iy_ix_i^T\alpha_jy_jx_j + \sum\limits_{i=1}^{m}\alpha_i \end{align} \\$

调一下顺序

$\min _ { w , b } \max _ { \alpha _ { i } \geq 0 } \mathcal { L } ( w , b , \alpha )= - \frac { 1 } { 2 } \sum _ { i = 1 , j = 1 } ^ { m } \alpha _ { i }\alpha _ { j } y _ { i }y _ { j } x _ { i } ^ { T } x _ { j } + \sum _ { i = 1 } ^ { m } \alpha _ { i } \\ \begin{array} { c } { \text {s.t.} , \alpha _ { i } \geq 0 , i = 1 , \ldots , n } \\ { \sum _ { i = 1 } ^ { n } \alpha _ { i } y = 0 } \end{array}$

这个$\alpha$是什么东西呢，其实就是如果$(x_i,y_i)$不是支持向量，那么它就是0，如果是就是一个非0的值。

$\max _ { \alpha _ { i } \geq 0 } \mathcal { L } ( w , b , \alpha ) = \max _ { \alpha _ { i } \geq 0 } \frac { 1 } { 2 } \| w \| ^ { 2 } - \sum _ { i = 1 } ^ { n } \alpha _ { i } \color{red}{ \left( y _ { i } \left( w ^ { T } x _ { i } + b \right) - 1 \right)}$

注意到如果 $x_i$ 是支持向量的话，上式中红颜色的部分是等于 0 的（因为支持向量的 functional margin 等于 1 ），而对于非支持向量来说，functional margin 会大于 1 ，因此红颜色部分是大于零的，而又是非负的，为了满足最大化，必须等于 0 。这也就是这些非Supporting Vector 的点的局限性。

求$\alpha$可以用SMO,KKT等方式，这就不说了太高深，这也不重要。

松弛变量

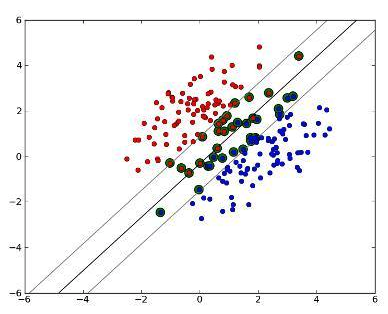
数据有的时候是线性可分，但是因为数据中总会有一些噪音的影响而导致线性不可分

为了处理这种情况，SVM 允许数据点在一定程度上偏离一下超平面。

我们原来的约束条件是

$y _ { i } \left( w ^ { T } x _ { i } + b \right) \geq 1 , \quad i = 1 , \ldots , n$

考虑到噪音

$y _ { i } \left( w ^ { T } x _ { i } + b \right) \geq 1 - \xi _ { i } , \quad i = 1 , \ldots , n$

其中$\xi _ { i } \ge 0$称为松弛变量 (slack variable) ,对应数据点$x_i$允许偏离的 functional margin 的量,那么

$\min \frac { 1 } { 2 } \| w \| ^ { 2 } + \color{red}{C \sum _ { i = 1 } ^ { n } \xi _ { i }} \\ \text {s.t.} \begin{array} { l } { y _ { i } \left( w ^ { T } x _ { i } + b \right) \geq 1 - \xi _ { i } , i = 1 , \ldots , n } \\ { \xi _ { i } \geq 0 , i = 1 , \ldots , n } \end{array}$

引入拉格朗日，最后结果为

$\max _ { \alpha } \sum _ { i = 1 } ^ { n } \alpha _ { i } - \frac { 1 } { 2 } \sum _ { i , j = 1 } ^ { n } \alpha _ { i } \alpha _ { j } y _ { i } y _ { j } \left\langle x _ { i } , x _ { j } \right\rangle \\ \begin{array} { c } { \text { s.t., } 0 \leq \alpha _ { i } \leq C , i = 1 , \ldots , n } \\ { \sum _ { i = 1 } ^ { n } \alpha _ { i } y _ { i } = 0 } \end{array}$

区别就在于多了一个上限$C$

kernel

kernel又是干嘛的呢？

事实上，大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在。在上文中，我们已经了解到了SVM处理线性可分的情况，那对于非线性的数据SVM咋处理呢？对于非线性的情况，SVM 的处理方法是选择一个核函数 $k(⋅,⋅)$ 通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。

这里有个很简单的思想

首先使用一个非线性映射将数据变换到一个特征空间F，使其线性可分，
然后在特征空间使用线性学习器分类。

也就是非线性数据，就找一个映射$k(·，·)$，然后一股脑把原来的数据映射到新空间中，再做线性 SVM 即可。不过事实上好像并没有这么简单。

如果原始空间是三维（一阶、二阶和三阶的组合），那么我们会得到：3(一次)+3(二次交叉)+3(平方)+3(立方)+1(x1x2x3)+23(交叉，一个一次一个二次，类似x1x2^2) = 19维的新空间，这个数目是呈指数级爆炸性增长的，从而势必这给的计算带来非常大的困难，而且如果遇到无穷维的情况，就根本无从计算了。

kernel则是直接在原来的低维空间中进行计算，而不需要显式地写出映射后的结果，也就是直接将$k(x_i,x_j)$视为新空间中的$x_ix_j$

那么

$min(L)= - \frac { 1 } { 2 } \sum _ { i = 1 , j = 1 } ^ { m } \alpha _ { i }\alpha _ { j } y _ { i }y _ { j } x _ { i } ^ { T } x _ { j } + \sum _ { i = 1 } ^ { m } \alpha _ { i } \\ \Downarrow \\ min(L)= - \frac { 1 } { 2 } \sum _ { i = 1 , j = 1 } ^ { m } \alpha _ { i }\alpha _ { j } y _ { i }y _ { j } k(x_i,x_j)+ \sum _ { i = 1 } ^ { m } \alpha _ { i }$

这样一来计算的问题就算解决了，避开了直接在高维空间中进行计算，而结果却是等价的！

但是kernel的选择确实很困难的，一般会采用以下几种

多项式核

$\kappa ( x , y ) = \left( a x ^ { T } y + c \right) ^ { d }$

高斯核

$\kappa \left( x _ { 1 } , x _ { 2 } \right) = \exp \left( - \frac { \left\| x _ { 1 } - x _ { 2 } \right\| ^ { 2 } } { 2 \sigma ^ { 2 } } \right)$

线性核

$\kappa \left( x _ { 1 } , x _ { 2 } \right) = \left\langle x _ { 1 } , x _ { 2 } \right\rangle$